This method introduced by Muller-Gartner et al. [5] is based on the assumption that white matter (WM) uptake is homogeneous, whereas the uptake in grey matter (GM) is variable in each pixel. All brain pixels are classified as white matter or grey matter and sorted into respective segments. Based on these segments and the assumed PET resolution the spill-out from WM to GM can be estimated and subtracted. Similarly, the spill-out from GM to the surroundings can be estimated and compensated for. The result is a grey matter image with corrected activity values in all pixels.
The following correction formula is applied:
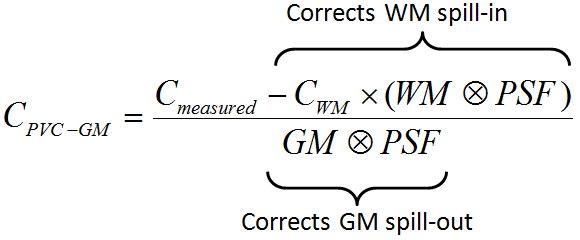
with the following notations:
CPVC-GM |
Corrected activity concentration. This is the result of the PVC correction in each GM pixel. |
Cmeasured |
Actually measured activity concentration in a GM pixel which may be distorted due to spill-out and spill-in. |
CWM |
Activity concentration in WM which is assumed to be homogeneous and just blurred by the PSF. |
WM, GM |
WM (GM) segment image which represents the WM (GM) probability of each pixel in the image as a value between 0 and 1. These images are assumed to represent the true anatomy with ideal resolution. |
PSF |
Point-spread function of the imaging system which is assumed to be constant across the image and represented by a three-dimensional Gaussian function. |
WM⊗PSF |
Mathematical convolution of the WM segment image with the PSF. The result represents the image of the ideal WM segment when detected with a real imaging system characterized by the PSF function.
The expected WM image is obtained by scaling WM⊗PSF by the WM concentration CWM. It is subtracted from the measured image to compensate for spill-in from WM to GM. |
GM⊗PSF |
Mathematical convolution of the GM segment image with the PSF.
A division of the WM-corrected image by GM⊗PSF represents a deconvolution operation and corrects for the spill-out effect from GM. The operation of division may introduce over-corrections at the GM boundary. Therefore, the result image is masked at a certain threshold of the convolved GM image |
Schematic of the Correction Workflow
The following illustration provides a graphical overview of the different processing steps as well as the resulting intermediate images.
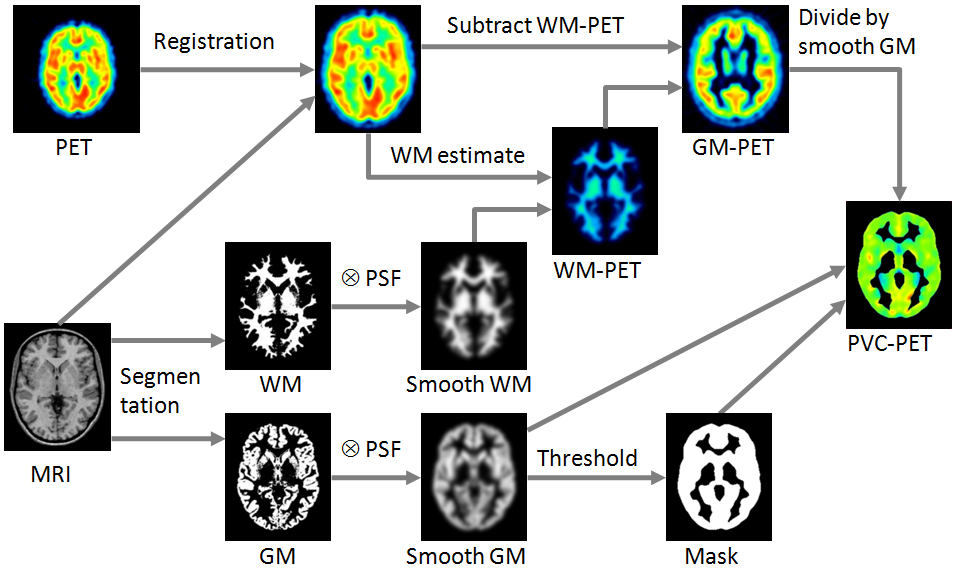
White-Matter Estimate and Masking
Three variants are available for the white matter uptake, which is used to scale the smoothed WM mask: Default is the regression approach of Giovacchini et al. [6]. It collects the PET uptake of all pixels with a WM probability higher than the specified value (e.g. 0.95), and performs a linear regression to estimate the WM value at the probability of 1. A first alternative is calculating the average value of all WM pixels. A second alternative is a fixed value manually entered by the user.
The PVC algorithm is only appropriate for GM pixels. All other pixels in the corrected image should therefore not be evaluated and should be masked. Therefore, a GM threshold should be specified. It is applied to the convolved GM segment (GM⊗PSF) in order to mask background and WM. Note that if the threshold is small, outlier values might appear along the mask boundaries as over-correction artifacts.

