The Fractal Dimension model measures the complexity of a 2-dimensional structure by calculating its box-counting dimension [1]. This concept has been applied in oncologic studies for assessing the heterogeneity of tissue kinetics [2].
The idea is to subdivide the area under the tissue TAC into a number of square boxes and simply count the number of boxes containing some part of the structure. The mesh size is defined as s, so 1/s gives the number of segments in each of the 2 dimensions. For instance, specifying 1/s=5 therefore means a subdivision into 5*5=25 boxes.
The counting process is performed with increasing number of intervals up to the specified 1/s. Next, the data are plotted in a double-logarithmic way, namely log(N(s)) on the y axis and log(1/s) on the x-axis.
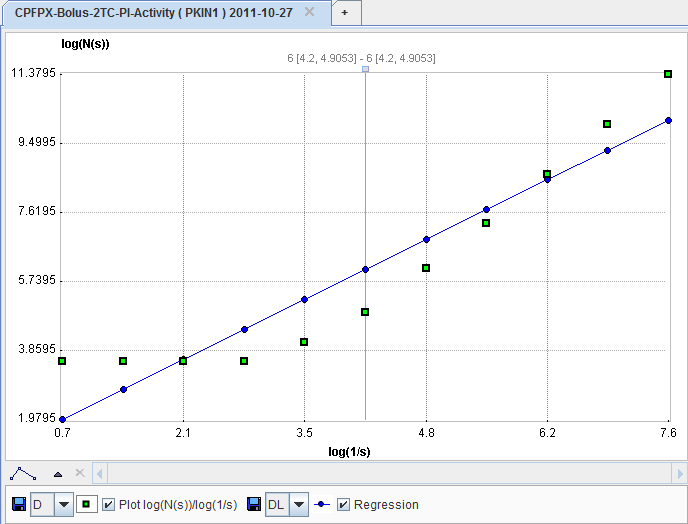
The box-counting dimension is finally obtained as the slope of a linear regression through the plotted points.
Implementation
After switching to the Fractal dimension model, two input parameters are available for specifying the box-counting process: 1/s, and Maximal value the highest TAC value which might occur in the data.
Acquisition and Data Requirements
Image Data |
Any dynamic volume data. Note that the time information is relevant for the results. |
Model Preprocessing
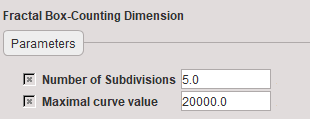
Number of subdivisions |
Maximal number of interval subdivisions in boxplot; 1/s=5 means 1/(25) intervals |
Maximal curve value |
The global maximal value. It is corrected upwards if the actual curve maximum exceeds this value. Note that the total area is relevant for the box subdivisions. To cover the same area for all TACs a common maximum value is required. |
Model Configuration
![]()
Db |
Box-counting dimension calculated with boxplot method. |
References
1.Peitgen H-O, Jürgens H, Saupe D: Chaos and fractals : new frontiers of science. New York: Springer-Verlag; 1992.
2.Strauss LG, Dimitrakopoulou-Strauss A, Koczan D, Bernd L, Haberkorn U, Ewerbeck V, Thiesen HJ: 18F-FDG kinetics and gene expression in giant cell tumors. J Nucl Med 2004, 45(9):1528-1535.